Next: 5.3.4 Peak Fitting Up: 5.3 JUSO Setup Previous: 5.3.2 Time Of Flight Contents
Two procedures were used to determine the detection efficiency of the microsphere plates in the JUSO setup as well as the overall detection efficiency.
For the first procedure the ion beam had to be directly deflected
into the TOF tube. As the angle between the TOF axis and the nominal
beam axis was only 10
![]() this could be done using the pair
of deflection plates closest to the sample. By varying the postacceleration
voltage of the TOF tube the energy of the particles could be adjusted
over a large range without having to change the settings of the sector
magnet. Assuming a constant beam intensity an energy range of
this could be done using the pair
of deflection plates closest to the sample. By varying the postacceleration
voltage of the TOF tube the energy of the particles could be adjusted
over a large range without having to change the settings of the sector
magnet. Assuming a constant beam intensity an energy range of ![]() 2keV
could be covered with
2keV
could be covered with ![]() being the energy of the primary
beam. However it was shown that not all particles would hit the detector
if the beam gets decelerated in the postacceleration stage due to
the beam divergence combined with the miss alignment of the beam [14].
Thus the detection efficiency would be underestimated for energies
below
being the energy of the primary
beam. However it was shown that not all particles would hit the detector
if the beam gets decelerated in the postacceleration stage due to
the beam divergence combined with the miss alignment of the beam [14].
Thus the detection efficiency would be underestimated for energies
below ![]() (Figure 5.3).
(Figure 5.3).

|
The main problem with the method described above is that the primary beam is not aligned with the TOF tube axis. The only particle source with perfect alignment in the setup is the investigated surface itself. Using the surface also allows to use the atoms instead of molecules for the calibration. Primary atom beams were too weak to be used with the method described above.
For detection efficiency measurements using the surface a low energy
(molecular) beam is used. The molecules dissociate during the interaction
with the surface. At the selected energy a constant but unknown fraction
of atoms ![]() get negatively ionized. The neutral part of
the beam entering the TOF tube serves as an intensity reference. By
applying different positive postacceleration voltages (such that the
particles get accelerated) the ion peak in the TOF spectra varies
in size and position depending on the energy of the ions after postacceleration.
The geometry of the aperture in front of the postacceleration stage
ensures that the particle flux into the tube is limited by this aperture
and does not depend on the value of the (positive) post acceleration
voltage. The peaks in the TOF spectra were then fitted using the function
described in Chapter 5.3.4. Usually four spectra
(s
get negatively ionized. The neutral part of
the beam entering the TOF tube serves as an intensity reference. By
applying different positive postacceleration voltages (such that the
particles get accelerated) the ion peak in the TOF spectra varies
in size and position depending on the energy of the ions after postacceleration.
The geometry of the aperture in front of the postacceleration stage
ensures that the particle flux into the tube is limited by this aperture
and does not depend on the value of the (positive) post acceleration
voltage. The peaks in the TOF spectra were then fitted using the function
described in Chapter 5.3.4. Usually four spectra
(s![]() to s
to s![]() ) were used for the further calculations
with s
) were used for the further calculations
with s![]() the spectra with the lowest and s
the spectra with the lowest and s![]() the
spectra with the highest post acceleration voltage.
the
spectra with the highest post acceleration voltage. ![]() denotes
the measured fraction of neutral atoms,
denotes
the measured fraction of neutral atoms, ![]() the measured
fraction of negatively ionized atoms of the n
the measured
fraction of negatively ionized atoms of the n![]() spectra
(
spectra
(![]() +
+ ![]() = 1, the possible small positive ion
fraction was neglected). With
= 1, the possible small positive ion
fraction was neglected). With ![]() denoting the unknown detection
efficiency for neutral atoms and
denoting the unknown detection
efficiency for neutral atoms and ![]() the detection efficiency
for postaccelerated ions in the n
the detection efficiency
for postaccelerated ions in the n![]() spectra the true ionization
efficiency
spectra the true ionization
efficiency ![]() of the surface may be written as:
of the surface may be written as:
Assuming that the detection efficiency for the most accelerated ions
in spectra 4 is close to one (![]()
![]() 1) , the
equation with n=4 simplifies to:
1) , the
equation with n=4 simplifies to:
Using ![]() +
+ ![]() = 1 and
= 1 and
![]() the
system 5.4 is solved for
the
system 5.4 is solved for ![]() to
to ![]() :
:
 |
(5.6) | ||
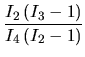 |
(5.7) | ||
| (5.8) | |||
| (5.9) |
The value of ![]() represents the relative detection efficiency
for ions at the energy
represents the relative detection efficiency
for ions at the energy
![]() with
with ![]() denoting the energy of a primary atom and
denoting the energy of a primary atom and ![]() the
energy gain due to the postacceleration used when acquiring the spectra
the
energy gain due to the postacceleration used when acquiring the spectra
![]() . All results for
. All results for ![]() were verified in a second
peak fitting run with appropriate weighting of the energy spectra
according to the calculated detection efficiencies. In this second
run where
were verified in a second
peak fitting run with appropriate weighting of the energy spectra
according to the calculated detection efficiencies. In this second
run where ![]() and
and ![]() were replaced by the true
(corrected) charge state fractions, all
were replaced by the true
(corrected) charge state fractions, all ![]() should evaluate
close to one. This was always the case within an error of a few percent.
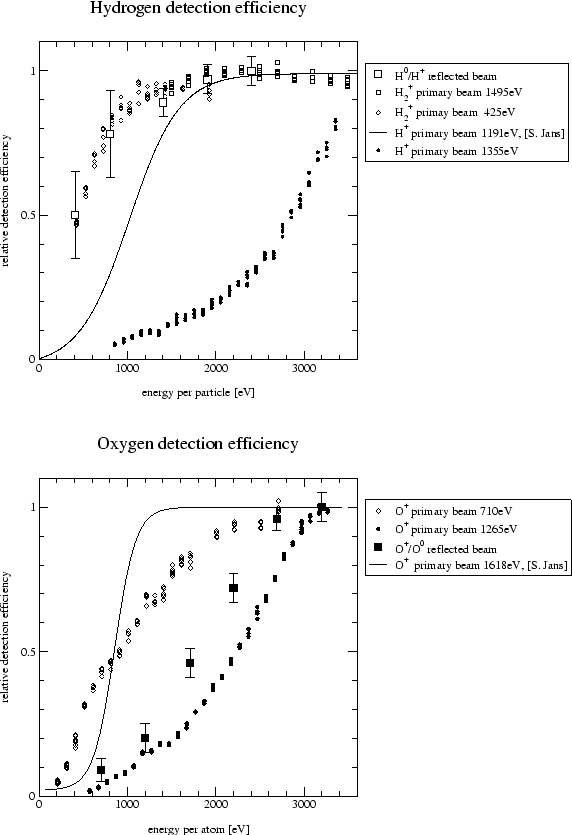
Detection efficiencies measured using the two procedures are shown
in Figure 5.4.
should evaluate
close to one. This was always the case within an error of a few percent.
Detection efficiencies measured using the two procedures are shown
in Figure 5.4.
Furthermore, assuming no significant difference in the MSP detection
efficiency between neutral and negatively charged particles (see below
for discussion) in the investigated energy range the detection efficiency
![]() may be extrapolated from the detection efficiencies for
ions. The value of
may be extrapolated from the detection efficiencies for
ions. The value of ![]() then allows the estimation of the
true ionization efficiency
then allows the estimation of the
true ionization efficiency ![]() of the surface at the energy
of the surface at the energy ![]() using:
using:
| (5.10) |
The efficiencies vary considerably depending on the procedure used. Because of the better geometric alignment, the values measured using the reflected beam are considered to be more accurate.
|
The values measured for hydrogen on the 'new' MSP seem to agree well (top plate in Figure 5.4). The efficiencies measured using the primary beam and the 'old' MSP on the other hand do not seem to be correct. When calculating ionization efficiencies on the same surface at the same energy from measurements taken with the 'old' and the 'new' MSP large discrepancies arise. When correcting the measurements taken with the 'old' MSP with the detection efficiency taken from [14] the ionization yields agree much better. A possible cause of this difference might be mechanical misalignment of the TOF tube. The TOF tube is attached by bellows to the target chamber and might therefore have been accidently moved. The data measured using the 'old' MSP were corrected by the efficiencies taken from [14], the data measured with the 'new' MSP were corrected by the detection efficiencies measured using the reflected beam.
The values measured for oxygen for the 'old' MSP using the primary and a reflected beam agree pretty well. But the detection efficiencies taken from [14] (line in bottom plate in Figure 5.4) measured one year ago were significantly better although it was already concluded in [14] that this efficiency curve was wrong. The differences might again be due to a mechanical displacement of the TOF tube, or the MSP might have deteriorated due to measurements done meanwhile. Interestingly even the 'new' MSP did not achieve the performance measured one year ago on the 'old' MSP. Unfortunately no data using a reflected oxygen beam is available. The oxygen data measured using the 'old' MSP was corrected using detection efficiencies measured using a reflected beam, data measured using the 'new' had to be corrected by detection efficiency data measured using a deflected primary beam as there is no data from a reflected oxygen beam available.
The detection efficiency for carbon ions was only measured using the
primary beam deflected onto the 'old' MSPs. The measured detection
efficiency was proportional to ![]() with
with ![]() denoting
the primary energy. There were doubts that these values represent
the true detection efficiency because they were very similar to the
efficiencies measured with H
denoting
the primary energy. There were doubts that these values represent
the true detection efficiency because they were very similar to the
efficiencies measured with H![]() primary beam that were found
to be inaccurate and also because the efficiencies for carbon were
expected to be somewhere in between those of hydrogen and oxygen.
Thus for carbon the detection efficiency of oxygen was used with twice
as large error bars to account for the uncertainties.
primary beam that were found
to be inaccurate and also because the efficiencies for carbon were
expected to be somewhere in between those of hydrogen and oxygen.
Thus for carbon the detection efficiency of oxygen was used with twice
as large error bars to account for the uncertainties.
Another source of error might be the different detection efficiencies for negative ions, positive ions and neutral atoms [22,23]. The detection efficiency for negative ions is higher than the efficiency for neutral atoms especially at lower energies. For the lowest energy used with oxygen (500eV per atom) the difference might be up to 30% and would lead to an overestimation of the negative ion fraction. As the detection efficiency is not well known at these energies anyway the influence of the charge state on the detection efficiency was neglected.
March 2001 - Martin Wieser, Physikalisches Institut, University of Berne, Switzerland