Figure 5.2: TOF geometry. The
dashed line depicts a particle path.

|
To convert the time of flight spectra to energy spectra the following
procedure was used [13
,26
,14
]. The time-of-flight  for a neutral particle scattered from the sample towards the detector
can be calculated as follows (Figure
5.2
):
for a neutral particle scattered from the sample towards the detector
can be calculated as follows (Figure
5.2
):

|
(5.1) |
where  is the particle mass and
is the particle mass and  the particle energy after reflection from the sample, and
the particle energy after reflection from the sample, and  is the sample - detector distance. The time-of-flight
is the sample - detector distance. The time-of-flight  of an accelerated ion is given by
of an accelerated ion is given by

|
(5.2) |
where 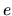 is the elementary charge,
is the elementary charge,  the length of the tube at postacceleration potential and
the length of the tube at postacceleration potential and  the postacceleration voltage. The TOF system was calibrated for each
new primary beam energy and particle mass. This was done by deflecting the
positive primary beam directly into the TOF tube. We then performed a first
measurement without postacceleration (thus yielding a time of flight according
to Equation 5.1
) and a second one with a certain postacceleration voltage (usually
the postacceleration voltage. The TOF system was calibrated for each
new primary beam energy and particle mass. This was done by deflecting the
positive primary beam directly into the TOF tube. We then performed a first
measurement without postacceleration (thus yielding a time of flight according
to Equation 5.1
) and a second one with a certain postacceleration voltage (usually  2000V) giving a time of flight according to Equation
5.2
. The two time-of-flights were measured with respect to an arbitrarily chosen
reference time
2000V) giving a time of flight according to Equation
5.2
. The two time-of-flights were measured with respect to an arbitrarily chosen
reference time  , which corresponded with the start time of the particle bunch at the
chopper. The difference
, which corresponded with the start time of the particle bunch at the
chopper. The difference  of the two time-of-flights was then calculated. From the equation
of the two time-of-flights was then calculated. From the equation
 the primary energy
the primary energy  was then calculated by solving Equations
5.2
and 5.1
numerically. Using Equation
5.1
the time of flight axis could the be calibrated.
was then calculated by solving Equations
5.2
and 5.1
numerically. Using Equation
5.1
the time of flight axis could the be calibrated.
As we never observed molecules in the reflected beam all peaks in the
TOF spectra are from atomic species and could be separated easily with virtually
no overlap. An example spectrum showing a molecular peak species in the TOF
is shown in Figure 5.6
(taken from [27
]). For each different particle mass and charge state the corresponding
rates in the TOF spectra were converted to an energy spectrum using

|
(5.3) |
where  and
and 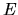 denote time and energy and
denote time and energy and  the count rate in energy and time space respectively, according to
the definition of distribution functions. The energy spectra obtained this
way were then corrected for detection efficiency.
the count rate in energy and time space respectively, according to
the definition of distribution functions. The energy spectra obtained this
way were then corrected for detection efficiency.
March 2001 - Martin Wieser, Physikalisches Institut, University
of Berne, Switzerland
![]() for a neutral particle scattered from the sample towards the detector
can be calculated as follows (Figure
5.2
):
for a neutral particle scattered from the sample towards the detector
can be calculated as follows (Figure
5.2
): ![]() and
and ![]() denote time and energy and
denote time and energy and ![]() the count rate in energy and time space respectively, according to
the definition of distribution functions. The energy spectra obtained this
way were then corrected for detection efficiency.
the count rate in energy and time space respectively, according to
the definition of distribution functions. The energy spectra obtained this
way were then corrected for detection efficiency.