Next: 5.3.6 Data Processing Up: 5.3 JUSO Setup Previous: 5.3.4 Peak Fitting Contents
The energy ![]() of the fragments in the laboratory frame
of a moving molecule that dissociates can be calculated using a Galilei
transformation [14]
of the fragments in the laboratory frame
of a moving molecule that dissociates can be calculated using a Galilei
transformation [14]
Assuming a uniform distribution of orientations of the molecules in
space and a constant value of ![]() , the broadening of the
energy distribution in the forward direction of the dissociated molecules
can be estimated:
, the broadening of the
energy distribution in the forward direction of the dissociated molecules
can be estimated:
Using spherical coordinates with the particle moving in +z direction
and an angle ![]() of the molecule axis to the z-axis, the
energy of the particle in +z direction is given by Equation 5.34.
With a uniform distribution of the molecule axis every direction has
the same probability
of the molecule axis to the z-axis, the
energy of the particle in +z direction is given by Equation 5.34.
With a uniform distribution of the molecule axis every direction has
the same probability ![]()
| (5.35) |
the solid angle ![]() may be expressed in terms of
may be expressed in terms of ![]() :
:
| (5.36) |
The probability
![]() for a particle to get the
energy
for a particle to get the
energy ![]() after dissociation is
after dissociation is
By substituting Equation 5.40 in Equation 5.39
and simplifying the energy distribution ![]() yields
yields
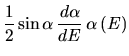 |
(5.41) | ||
 |
(5.42) |
This simple model assuming an uniform distribution of the molecule
axis yields a rectangular energy distribution in forward direction.
By extending Equation 5.20 a new fit function
was constructed consisting of a exponentional, a gaussian, and a rectangular
part (Equations 5.43 to 5.46).
![]() is the Heaviside step function and
is the Heaviside step function and ![]() denotes the full width of the rectangular part.
denotes the full width of the rectangular part.
March 2001 - Martin Wieser, Physikalisches Institut, University of Berne, Switzerland