4.2. 2 Reflection efficiency

To compare the different scattering properties of the investigated surfaces we define the reflection efficiency 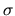as ratio of particles scattered inside the detection area of the MCP (approximately a cone of 12 half width) 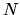to the total number of the particles .

$$\sigma \left( E\right) =\frac{N_{beam}}{N}$$

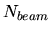The total particle flux 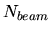is measured by the probe current. For early measurements a beam current larger than 0.1 pA had to be selected to get a reasonable quality of the probe current measurement. This beam current might already have led to saturation of the MCP for a highly reflective sample. Thus the approximately linear dependence of the beam current from the filament current in the ion source was used to determine the intensity of a weak beam: First the beam intensity was calibrated against the filament current at beam currents larger than 0.1 pA, then the resulting intensity was extrapolated to lower filament currents. Later a better pico-ampere-meter was installed with a lower usable threshold for the beam current of 0.02pA. This eliminated the need for the fitting procedure but no modifications were made to the software in order to maintain compatibility to older measurements. Figure 4.1 depicts a typical plot of such a fit.

The number of detected particles is calculated according to [ 14 ] by

$$N'=N\cdot \left\{ \left( 1-p_{D}\left( E\right) \right) \cdo... ...^{2}_{a}\left( \frac{E}{2}\right) \right] \right\} \cdot T^{3}$$ (4.1)

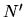• [ ]: Number of detected particles
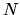• [ ]: Number of incident molecules or atom pairs after dissociation
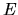• [ ]: Energy of primary molecules
• [ ]: dissociation probability for an incident molecule
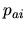• [ ]: probability for atoms to capture an electron
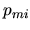• [ ]: probability for molecules to capture an electron
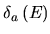• [ ]: absolute detection efficiency for atoms with energy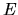
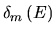• [ ]: absolute detection efficiency for molecules with energy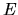
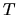• [ ]: transmission of one of three grids in front of the detector

The factor 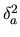accounts for the fact that both atoms of a dissociated molecule can not be detected simultaneously. For this calculation only neutral particles are considered. Negatively charged ions have a higher detection efficiency because of postacceleration in the MCP channels and their different secondary electron yield. The detection probability for a single neutral particle is approximately given by [12 ]

$$\delta _{[neutral]}\left( E\right) =A\cdot \left( 1-e^{-\gamma _{[neutral]}\left( E\right) }\right)$$ (4.2)

where 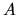is the fraction of the active area (the channel openings) of the MCP relative to the total detector area. 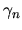denotes the secondary electron yield of the channel walls for a neutral particle. For negatively charged particles this equation changes to

$$\delta _{[negative]}\left( E\right) =A\cdot \left( 1-e^{-\gamma _{[negative]}\left( E+E_{p}\right) }\right)$$ (4.3)

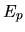with denoting the secondary electron yield for negatively charged particles and denoting the energy gain due to postacceleration of the particle in the channels. The postacceleration potential 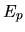is approximately 50eV [12 ] and can be ignored at higher energies. The charge dependence of the secondary electron yield was considered in [ 12 ,14 ,21 ] but the derived model became useless at energies below 200eV per atom. Recently data for detection efficiencies at low energies for oxygen [ 22 ] and hydrogen [23 ] became available. This data suggests a higher secondary electron yield for negatively charged particles in contradiction to the model used in [ 14 ]. However at the standard energy used for scattering and detection efficiency measurements (390eV per atom) the differences between and are small compared to the other sources of uncertainty independent of the model used and thus the values were assumed to be the same. For measurements of the charge state fraction described in Section 5.6.2 this assumption is no longer valid and the energy and charge state dependence of the detection efficiency has to be considered in more detail.

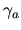Further calculation in [14 ], based on the assumption that an incident molecule produces the same number of secondary electrons as its equally fast constituents ( depicts the secondary electron yield for molecules and the secondary electron yield for atoms, respectively),

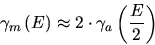
$$\gamma _{m}\left( E\right) \approx 2\cdot \gamma _{a}\left( \frac{E}{2}\right)$$ (4.4)

yields using Equation 4.2 :

$$\delta _{a}\left( E\right) = A\cdot \left( 1-e^{-\gamma _{a}\left( E\right) }\right)$$ (4.5)

$$\delta _{m}\left( E\right) = A\cdot \left( 1-e^{-\gamma _{m}\left( E\right) }\right) =A\cdot \left( 1-e^{-2\gamma _{a}\left( \frac{E}{2}\right) }\right)$$ (4.6)

These two equations can be combined to

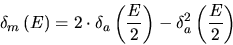
$$\delta _{m}\left( E\right) =2\cdot \delta _{a}\left( \frac{E}{2}\right) -\delta ^{2}_{a}\left( \frac{E}{2}\right)$$ (4.7)

and Equation 4.1 simplifies to

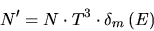
$$N'=N\cdot T^{3}\cdot \delta _{m}\left( E\right)$$ (4.8)

The value of 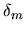is unfortunately not well known. A value of 0.36 was chosen for 780eV O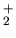 primary particles by [14 ]. Data taken from [22 ] suggests a value for 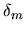of 0.45 at 780eV per molecule as calculated using Equation 4.7 but the uncertainties are rather high. For the present studies the 0.36 value was used to ensure the comparability with earlier results. For the comparison of different surfaces the exact value of 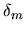has no influence anyway as long as the same value is used for all samples and no absolute values for the reflection efficiency are needed.

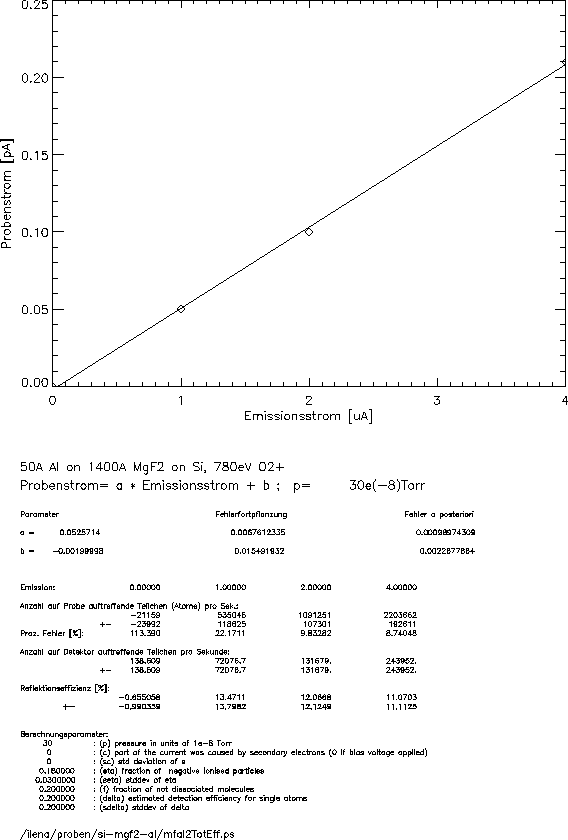
Figure 4.1: Sample output of the IDL script used to calculate the reflection efficiency. The viewgraph shown on top depicts the fit between the ion source filament current and the beam current. The reflection efficiency is shown in the line below the word Reflektionseffizienz.